Okay so we've done simple circles, and just like my old high school thought, that means we're ready for harder math.
"On a 2D screen, going from left to right, how would one calculate the arc trajectory of projectile that has weight, like a cannonball"
--- Action is in the stack script!
The value that the scrollbar adjusts will change according to the property selected in the Control field.
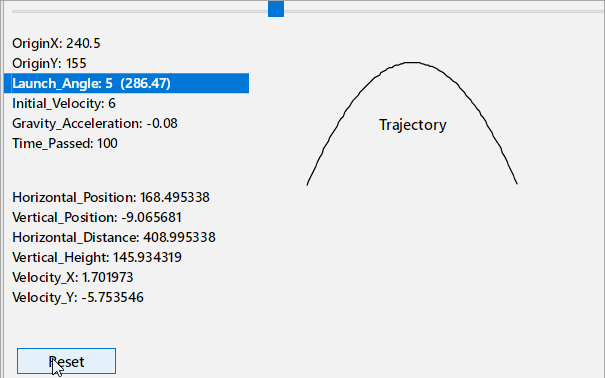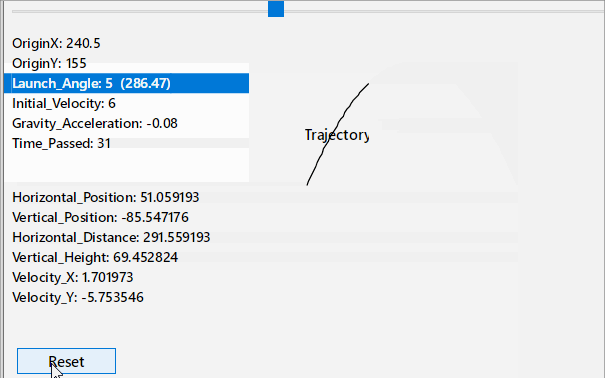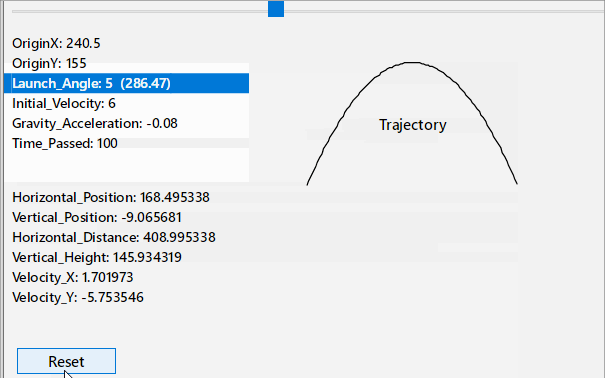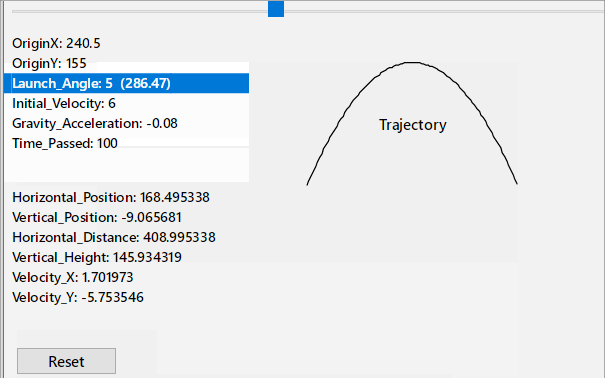
- Trajectory.gif (68.72 KiB) Viewed 2761 times
Here is a wikipedia article on "Artillery Games"
Example on Mac Classic
The classic
Scorched Earth computer game, which would inspired the
WORMS franchise.
And I'm like 80% sure this
scene from the Disney film TRON is based on the games made with this simulation.
Here is a resource for educators and students
Ok we are armed with context let's get to the science of it.
Calculating the arc trajectory of a projectile with weight, such as a cannonball, involves understanding its motion under the influence of gravity.
Trajectory Definition:
The trajectory, also known as the flight path, is the path followed by a moving object under the action of gravity.
For short distances, the trajectory of a projectile (like a cannonball) can be approximated by a parabola.
Equations of Motion:
We’ll use the following equations of motion:
(
h) = (x = V_x \cdot t) --- Horizontal Position
(
v) = (y = h + V_y \cdot t - \frac{g \cdot t^2}{2}) --- Vertical Position
(
x) represents the horizontal distance
(
y) represents the vertical height
(
V_x) is the horizontal velocity component.
(
V_y) is the vertical velocity component.
(
g) is the acceleration due to gravity.
(
t) is the time.
Velocity Components:
The horizontal velocity component ((
V_x)) is given by (
V_0 \cdot \cos(\alpha)).
The vertical velocity component ((
V_y)) is given by (
V_0 \cdot \sin(\alpha)), where:
(
V_0) is the initial velocity.
(
\alpha) is the launch angle.
Combined Formula:
Combining the equations of motion and velocity components, we get the trajectory formula:
[y = h + x \cdot \tan(\alpha) - \frac{g \cdot x^2}{2 \cdot V_0^2 \cdot \cos^2(\alpha)}]
Interpretation:
(
h) represents the initial height.
(
x) is the horizontal distance traveled.
(
\alpha) is the launch angle.
The term
(\frac{g \cdot x^2}{2 \cdot V_0^2 \cdot \cos^2(\alpha)}) accounts for the effect of gravity on the trajectory.
Easy.

Some not so obvious math concepts in that equation:
Let’s break down the mathematical notation in the trajectory formula:
The symbol (
\cdot) represents multiplication.
In the context of the trajectory formula, (
x \cdot \tan(\alpha)) means multiplying the horizontal distance (
x) by the tangent of the launch angle (
\alpha).
The expression (
\frac{g \cdot x^2}{2 \cdot V_0^2 \cdot \cos^2(\alpha)}) is a fraction.
Here’s what each part means:
(
g) represents the acceleration due to gravity.
(
x^2) is the square of the horizontal distance.
(
V_0) represents the initial velocity.
(
\cos^2(\alpha)) is the square of the cosine of the launch angle (
\alpha).
In summary, the trajectory formula combines these components to describe the path of a projectile (like a cannonball) considering both horizontal and vertical motion.
Note the weird curly braces in the equation...well:
Curly Braces Around the 2:
The curly braces ({}) around the 2 in the expression (\frac{g \cdot t^2}{2}) are not standard mathematical notation.
They might have been used for emphasis or clarity, but mathematically, they don’t change the meaning of the expression.
In programming, you can ignore these curly braces. The expression remains the same without them.
Okay...ignore curly braces.
Important note after like 3 hours of fighting this thing.
Gravity_Acceleration should be a negative value, that way it decelerates the object until the zenith and then causes it to plummet back to virtual earth. I asked ChatGPT four times how to get the arc to a target and it was like
"Trial and error" and
"Your code looks correct, except for everything you do to make your code make sense to anyone but a computer" Not one single time did it say
"You know if your Gravity_Acceleration is not negative, your projectile will fly off toward infinity rapidly and then turn around and smack in you the face before you see it coming"
Also, because ChatGPT chewed me out on this: a note about Globals in this stack and others I make.
Apparently, Globals are dangerous in bigger projects. But when I'm experimenting I can't stand having the Message Box pop open every time I want to check that a variable has as sensible value, and then having to hunt down all the stray "put" tstatements I placed to test values. So I pile on the Globals so I can see what they are doing when I want to see them. Also so I don't have to use massively long arguments in handlers like "Update all the fields that show global values with all these globals values" or packing things into custom proeprties and then pulling them out again. It's also something I picked up from games where you can set a global value in an in-game console and the whole program knows what you changed without any issues. An extra benefit is that when the Message Box does appear...it's because something has goofed in my code, like I forgot to finish a
Put line with an "
into something". Usually those kind of lines are some extreme test of all the values in a handler or function, like there's 10 things changing and one of them is wrong, but which one?